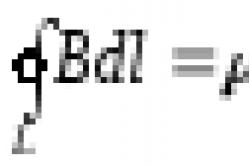Жаропонижающие средства для детей назначаются педиатром. Но бывают ситуации неотложной помощи при лихорадке, когда ребенку нужно дать лекарство немедленно. Тогда родители берут на себя ответственность и применяют жаропонижающие препараты. Что разрешено давать детям грудного возраста? Чем можно сбить температуру у детей постарше? Какие лекарства самые безопасные?
14) Потенциальная энергия заряда в электрическом поле. Работу, совершаемую силами электрического поля при перемещении положительного точечного заряда q из положения 1 в положение 2, представим как изменение потенциальной энергии этого заряда:
где Wп1 и Wп2 – потенциальные энергии заряда q в положениях 1 и 2. При малом перемещении заряда q в поле, создаваемом положительным точечным зарядом Q, изменение потенциальной энергии равно
При конечном перемещении заряда q из положения 1 в положение 2, находящиеся на расстояниях r1 и r2 от заряда Q,
Если поле создано системой точечных зарядов Q1, Q2,¼, Qn, то изменение потенциальной энергии заряда q в этом поле:
Приведённые формулы позволяют найти только изменение потенциальной энергии точечного заряда q, а не саму потенциальную энергию. Для определения потенциальной энергии необходимо условиться, в какой точке поля считать ее равной нулю. Для потенциальной энергии точечного заряда q, находящегося в электрическом поле, созданном другим точечным зарядом Q, получим
где C – произвольная постоянная. Пусть потенциальная энергия равна нулю на бесконечно большом расстоянии от заряда Q (при r ® ¥), тогда постоянная C = 0 и предыдущее выражение принимает вид
При этом потенциальная энергия определяется как работа перемещения заряда силами поля из данной точки в бесконечно удаленную. В случае электрического поля, создаваемого системой точечных зарядов, потенциальная энергия заряда q:
Потенциальная энергия системы точечных зарядов. В случае электростатического поля потенциальная энергия служит мерой взаимодействия зарядов. Пусть в пространстве существует система точечных зарядов Qi (i = 1, 2, ... , n). Энергия взаимодействия всех n зарядов определится соотношением
где r i j - расстояние между соответствующими зарядами, а суммирование производится таким образом, чтобы взаимодействие между каждой парой зарядов учитывалось один раз.
34. Магнитные взаимодействия: опыты Эрстеда и Ампера; магнитное поле; сила Лоренца, индукция магнитного поля; силовые линии магнитного поля; магнитное поле, создаваемое движущимся с постоянной скоростью точечным зарядом.
Магнитное поле - силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения , магнитная составляющая электромагнитного поля
Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, хотя в заметно меньшей степени) (постоянные магниты).
Опыт Эрстеда показал, что электрические токи могут действовать на магниты, однако природа магнита в то время была совершенно таинственной. Ампер и другие вскоре открыли взаимодействие электрических токов друг с другом, проявляющееся, в частности, как притяжение между двумя параллельными проводами, по которым текут одинаково направленные токи. Это привело Ампера к гипотезе, что в магнитном веществе имеются постоянно циркулирующие электрические токи. Если такая гипотеза справедлива, то результат опыта Эрстеда можно объяснить взаимодействием гальванического тока в проволоке с микроскопическими токами, которые сообщают стрелке компаса особые свойства
Сила Лоренца - сила, с которой, в рамках классической физики, электромагнитное поледействует на точечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью зарядлишь со сторонымагнитного поля, нередко же полную силу - со стороны электромагнитного поля вообще , иначе говоря, со стороны электрического имагнитного полей. Выражается вСИ как:
Для непрерывного распределения заряда, сила Лоренца принимает вид:
где d F - сила, действующая на маленький элемент dq .
ИНДУКЦИЯ МАГНИТНОГО ПОЛЯ -векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой магнитное поле действует назаряд , движущийся со скоростью.
Более конкретно, - это такой вектор, чтосила Лоренца , действующая со стороны магнитного поля на заряд , движущийся со скоростью, равна
где косым крестом обозначено векторное произведение, α - угол между векторами скорости и магнитной индукции (направление вектора перпендикулярно им обоим и направлено поправилу буравчика).
36. Действие магнитных полей на электрические токи: закон Био-Савара-Лапласа-Ампера и его применение для расчета силы, действующей со стороны однородного магнитного поля на отрезок тонкого прямого проводника с током; формула Ампера и ее значение в метрологии.
Рассмотрим произвольный проводник,в котором протекают токи:
dF =* ndV =* dV
З-н Био-Савара-Ампера для объемного тока:dF=jBdVsin. dF перпендикулярно ,т.е . направленно к нам. Возьмем тонкий проводник: , тогда для линейного эл-а тока з-н запишется в виде: dF = I , т.е. dF = IBdlsin .
Задача 1! Имеется однородное магнитное поле. В нем нах-я отрезок провода,который имеет l и I.
d = I , dF = IBdlsin , F = IBsin = IBlsin -сила Ампера.
1 Ампер-сила тока,при протекании которого по 2 || длинным,тонким проводникам,находящимся на расстоянии 1 м друг от друга действует сила равная 2*10^-7 Н на каждый метр их длины.
Задача 2! Есть 2 || длинных проводника, где l>> d ,тогда d =, dd , . Тогда ф-а Ампера: *l .
37. Магнитный диполь: физическая модель и магнитный момент диполя; магнитное поле, создаваемое магнитным диполем; силы, действующие со стороны однородного и неоднородного магнитных полей на магнитный диполь.
ДИПОЛЬ МАГНИТНЫЙ аналог диполя электрического, к-рый можно представлять себе как два точечных магн. заряда , расположенных на расстоянииl друг от друга. Характеризуется дипольным моментом, равным по величинеи направленным от.
Поля, создаваемые равными Д. м. вне области источников ввакууме (или в любой иной среде, магн. проницаемость к-рой =1), одинаковы, однако в средах ссовпадение достигается, если только принять, что, т. е. считать, что дипольный момент зарядового Д. м. зависит от проницаемости
38. Теорема Гаусса для магнитного поля: интегральная и дифференциальная формы, физический смысл теоремы. Релятивистский характер магнитного поля: магнитные взаимодействия как релятивистское следствие электрических взаимодействий; взаимные преобразования электрических и магнитных полей.
Отсутствие в природе магнитных зарядов приводит к тому, что линии вектора В не имеют ни начала, ни конца. Поток вектора В через замкнутую поверхность должен быть равен нулю. Таким образом, для любого магнитного поля и произвольной замкнутой поверхности S имеет место условие
Эта формула выражает теорему Гаусса для вектора В : поток вектора магнитной индукции через любую замкнутую поверхность равен нулю.
В интегральной форме
1. Поток вектора электрического смещения через любую замкнутую поверхность, окружающую некоторый объем, равен алгебраической сумме свободных зарядов, находящихся внутри этой поверхности
Вектор – это такая характеристика поля, которая не зависит от диэлектрических свойств среды.
В дифференциальной форме
Пусть в объеме имеется
где - средняя по объему плотность. Тогда
При стягивании объема в точку
- теорема Гаусса в дифференциальной форме
39. Теорема о циркуляции вектора магнитной индукции стационарного магнитного поля для вакуума: интегральная и дифференциальная формы, физический смысл теоремы; применение теоремы для расчета магнитных полей на примере магнитного поля, создаваемого бесконечно длинным соленоидом с током.
Теорема. Циркуляция вектора магнитной индукции В по замкнутому контуру L равна алгебраической сумме токов, охватываемых данным контуром L , умноженной на μ 0 .
Примеры:
![]()
I 3
I 1 I 2
– ток за пределами контура.
Применяя принцип суперпозиции к магнитным полям, получаем:
Если токи протекают в сплошной среде, получаем:
Теорема Стокса:где S -поверхность ограниченная контуром L .
- теорема о циркуляции вектора магнитной индукции.
для электростатического поля
электростатическое поле – потенциальное, имеются источники поля – заряды.
2) для магнитного поля
магнитное поле – не потенциальное, а вихревое, нет магнитных зарядов.
Соленоид – катушка с плотнонамотанными друг к другу витками на цилиндрический сердечник, при этом l >> D (если соленоид считать бесконечным).
- индукция магнитного поля
тороида, где n – число витков на единицу длины осевой линии
40. Магнетики. Намагничивание вещества: физическая сущность явления; гипотеза Ампера о молекулярных токах; токи намагничивания, намагниченность (вектор намагничивания); связь вектора намагничивания с поверхностными и объемными токами намагничивания.
Магнетики – вещества, способные намагничиваться, если их поместить во внешнее электрическое поле. Атомы обладают магнитными моментами. При отсутствии внешнего магнитного поля магнитные моменты атомов ориентированы хаотически и суммарный магнитный момент вещества равен нулю. При внесении вещества во внеш. магн. поле, магн. моменты атомов ориентированы преимущественно в одном направлении, вследствие чего суммарный момент отличен от нуля и вещество намагничивается. Степень намагниченности магнетиков характеризуется величиной:
Намагниченность магнетика (вектор намагниченности)
Намагниченное вещество создает собственное магнитное поле с индукцией B 0 , тогда индукция результирующего магнитного поля
Намагниченность магнетика
В 0 цилиндрической формы
Напряженность магнитного поля
x<0, μ<1 – диамагнетики
x>0, μ>1 – парамагнетики
x>>0, μ>>1 – ферромагнетики
Диамагнетики – вещества, магнитные моменты атомов которых, при отсутствии внешнего магнитного поля равны нулю (цветные газы, стекло, вода, золото, серебро, медь, ртуть). Для диамагнетиков магнитная восприимчивость не зависит от температуры.
Парамагнетики – вещества, магнитные моменты атомов которых, отличны от нуля (кислород, окись азота, алюминий, платина)
Ампер предположил, что внутри вещества циркулируют некоторые токи, которые он назвал молекулярными- это токи связанные с орбитальным движением электронов.
Т.О. каждый электрон, который движется по орбите атома создаёт свой ток.
Действие магнитного поля на проводник с током. З-н Ампера.
Покажем, что з-н Ампера вытекает из силы Лоренца. На каждую заряженную частицу действует сила Лоренца.
Вычислим силу, действующую на элемент
Сила на элемент тока
Сила, действующая
на элемент проводника с
током, сила Ампера.
45 Электромагнитная индукция: опыты Фарадея по электромагнитной индукции; физическая сущность явления; закон электромагнитной индукции Фарадея и его физическое обоснование, правило Ленца; принцип действия флюксметра.
Открыто Фарадеем в 1831 г. Электромагнитной индукцией называется явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока пронизывающего данный контур.
ЭДС электромагнитной индукции.
Правило Ленца: индукционный ток имеет такое направление, что его магнитное поле противодействует изменению магнитного потока, вызывающего данный ток.
– з-н электромагнитной индукции (з-н Фарадея).
Токи Фуко – вихревые токи, возникающие в проводящей среде при изменении магнитного потока, пронизывающего эту среду.
Величина токов Фуко зависит от частоты
изменения магнитного потока и
сопротивления материала. Вихревые токи
Фуко нагревают массивный проводник.
Потокосцепление. Индуктивность контура. Индуктивность соленоида.
N B Пусть имеется соленоид.
(магнитный поток, связанный
I с одним витком).
– потокосцепление , магнитный поток, связанный со всеми витками. Опытами установлено, что потокосцепление пропорционально току:
– индуктивность
– индукция магнитного поля соленоида.
– индуктивность соленоида, где
| " |
Принцип суперпозиции.
Если с помощью пробного заряда исследуется электрическое поле, создаваемое несколькими заряженными телами, то результирующая сила оказывается равной геометрической сумме сил, действующих на пробный заряд со стороны каждого заряженного тела в отдельности. Следовательно, напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряжённостей электрических полей, создаваемых в той же точке зарядами в отдельности:
Это свойство электрического поля означает, что поле подчиняется принципу суперпозиции . В соответствии с законом Кулона, напряженность электростатического поля, создаваемого точечным зарядом Q на расстоянии r от него, равна по модулю:

Это поле называется кулоновским. В кулоновском поле направление вектора напряженности зависит от знака заряда Q: если Q больше 0, то вектор напряженности направлен от заряда, если Q меньше 0, то вектор напряженности направлен к заряду. Величина напряжённости зависит от величины заряда, среды, в которой находится заряд, и уменьшается с увеличением расстояния.
Напряженность электрического поля, которую создает заряженная плоскость вблизи своей поверхности:
Итак, если в задаче требуется определить напряженность поля системы зарядов, то надо действовать по следующему алгоритму:
1. Нарисовать рисунок.
2. Изобразить напряженность поля каждого заряда по отдельности в нужной точке. Помните, что напряженность направлена к отрицательному заряду и от положительного заряда.
3. Вычислить каждую из напряжённостей по соответствующей формуле.
4. Сложить вектора напряжённостей геометрически (т.е. векторно).
Потенциальная энергия взаимодействия зарядов.
Электрические заряды взаимодействуют друг с другом и с электрическим полем. Любое взаимодействие описывает потенциальной энергией. Потенциальная энергия взаимодействия двух точечных электрических зарядов рассчитывается по формуле:
Обратите внимание на отсутствие модулей у зарядов. Для разноименных зарядов энергия взаимодействия имеет отрицательное значение. Такая же формула справедлива и для энергии взаимодействия равномерно заряженных сфер и шаров. Как обычно, в этом случае расстояние r измеряется между центрами шаров или сфер. Если же зарядов не два, а больше, то энергию их взаимодействия следует считать так: разбить систему зарядов на все возможные пары, рассчитать энергию взаимодействия каждой пары и просуммировать все энергии для всех пар.
Задачи по данной теме решаются, как и задачи на закон сохранения механической энергии: сначала находится начальная энергия взаимодействия, потом конечная. Если в задаче просят найти работу по перемещению зарядов, то она будет равна разнице между начальной и конечной суммарной энергией взаимодействия зарядов. Энергия взаимодействия так же может переходить в кинетическую энергию или в другие виды энергии. Если тела находятся на очень большом расстоянии, то энергия их взаимодействия полагается равной 0.
Обратите внимание: если в задаче требуется найти минимальное или максимальное расстояние между телами (частицами) при движении, то это условие выполнится в тот момент времени, когда частицы движутся в одну сторону с одинаковой скоростью. Поэтому решение надо начинать с записи закона сохранения импульса, из которого и находится эта одинаковая скорость. А далее следует писать закон сохранения энергии с учетом кинетической энергии частиц во втором случае.
В пределах электростатики невозможно дать ответ на вопрос, где сосредоточена энергия конденсатора. Поля и заряды, их образовавшие, не могут существовать обособленно. Их не разделить. Однако переменные поля могут существовать независимо от возбуждавших их зарядов (излучение солнца, радиоволны, …), и они переносят энергию. Эти факты заставляют признать, что носителем энергии является электростатическое поле .
При перемещении электрических зарядов силы кулоновского взаимодействия совершают определенную работу dА . Работа, совершенная системой, определяется убылью энергии взаимодействия -dW зарядов
| . | (5.5.1) |
Энергия взаимодействия двух точечных зарядов q 1 и q 2 , находящихся на расстоянии r 12 , численно равна работе по перемещению заряда q 1 в поле неподвижного заряда q 2 из точки с потенциалом в точку с потенциалом :

![]()

| . | (5.5.2) |
Удобно записать энергию взаимодействия двух зарядов в симметричной форме
| (5.5.3) |
Для системы из n точечных зарядов (рис. 5.14) в силу принципа суперпозиции для потенциала, в точке нахождения k -го заряда, можно записать:
Здесь φ k , i - потенциал i -го заряда в точке расположения k -го заряда. В сумме исключен потенциал φ k , k , т.е. не учитывается воздействие заряда самого на себя, равное для точечного заряда бесконечности.

Тогда взаимная энергия системы n зарядов равна:
| (5.5.4) |
Данная формула справедлива лишь в случае, если расстояние между зарядами заметно превосходит размеры самих зарядов.
Рассчитаем энергию заряженного конденсатора. Конденсатор состоит из двух, первоначально незаряженных, пластин. Будем постепенно отнимать у нижней пластины заряд dq и переносить его на верхнюю пластину (рис. 5.15).

В результате между пластинами возникнет разность потенциалов При переносе каждой порции заряда совершается элементарная работа
![]()
Воспользовавшись определением емкости получаем
Общая работа, затраченная на увеличение заряда пластин конденсатора от 0 до q , равна:
Эту энергию можно также записать в виде
(Краткие теоретические сведения)
Энергия взаимодействия точечных зарядов
Энергия взаимодействия системы точечных зарядов равна работе внешних сил по созданию данной системы (см. рис.1) посредством медленного (квазистатического) перемещения зарядов из бесконечно удаленных друг от друга точек в заданные положения. Эта энергия зависит только от конечной конфигурации системы, но не от способа, каким эта система была создана.
Основываясь на таком определении, можно получить следующую формулу для энергии взаимодействия двух точечных зарядов, расположенных в вакууме на расстоянии r 12 друг от друга:
 .
(1)
.
(1)
Если система содержит три неподвижных точечных заряда, то энергия их взаимодействия равна сумме энергий всех парных взаимодействий:
где r 12 – расстояние между первым и вторым, r 13 - между первым и третьим, r 23 – между вторым и третьим зарядами. Аналогично вычисляется электрическая энергия взаимодействия системы из N точечных зарядов:
Например, для системы из 4-х зарядов формула (2) содержит 6 слагаемых.
Электрическая энергия заряженных проводников
Электрическая энергия уединенного заряженного проводника равна работе, которую нужно совершить, чтобы нанести на проводник данный заряд, медленно перемещая его бесконечно малыми порциями из бесконечности, где изначально эти порции заряда не взаимодействовали. Электрическую энергию уединенного проводника можно вычислить по формуле
 ,
(3)
,
(3)
где q
– заряд проводника, - его
потенциал. В частности, если заряженный
проводник имеет форму шара и расположен
в вакууме, то его потенциал
 и, как следует из (3), электрическая
энергия равна
и, как следует из (3), электрическая
энергия равна
 ,
,
где R – радиус шара, q – его заряд.
Аналогично определяется электрическая энергия нескольких заряженных проводников – она равна работе внешних сил по нанесению данных зарядов на проводники. Для электрической энергии системы из N заряженных проводников можно получить формулу:
 ,
(4)
,
(4)
где
 и
и
 - заряд
и потенциал
- заряд
и потенциал
 -
го
проводника. Заметим, что формулы (3), (4)
справедливы и в том случае, когда
заряженные проводники находятся не в
вакууме, а в изотропном нейтральном
диэлектрике.
-
го
проводника. Заметим, что формулы (3), (4)
справедливы и в том случае, когда
заряженные проводники находятся не в
вакууме, а в изотропном нейтральном
диэлектрике.
При помощи (4) вычислим электрическую энергию заряженного конденсатора . Обозначив заряд положительной обкладки q , ее потенциал 1 , а потенциал отрицательной обкладки 2 , получим:
 ,
,
где
 - напряжение на конденсаторе. Учитывая,
что
- напряжение на конденсаторе. Учитывая,
что
 ,
формулу для энергии конденсатора можно
представить также в виде
,
формулу для энергии конденсатора можно
представить также в виде
 ,
(5)
,
(5)
где C – емкость конденсатора.
Собственная электрическая энергия и энергия взаимодействия
Рассмотрим электрическую энергию двух проводящих шаров, радиусы которых R 1 , R 2 , а заряды q 1 , q 2 . Будем считать, что шары расположены в вакууме на большом по сравнению с их радиусами расстоянии l друг от друга. В этом случае расстояние от центра одного шара до любой точки поверхности другого примерно равно l и потенциалы шаров можно выразить формулами:
 ,
,
 .
.
Электрическую энергию системы найдем при помощи (4):
 .
.
Первое слагаемое в полученной формуле – энергия взаимодействия зарядов, расположенных на первом шаре. Эту энергию называют собственной электрической энергией (первого шара). Аналогично, второе слагаемое – собственная электрическая энергия второго шара. Последнее слагаемое – энергия взаимодействия зарядов первого шара с зарядами второго.
При
 электрическая энергия взаимодействия
существенно меньше суммы собственных
энергий шаров, однако при изменении
расстояния между шарами собственные
энергии остаются практически постоянными
и изменение полной электрической энергии
примерно равно изменению энергии
взаимодействия. Этот вывод справедлив
не только для проводящих шаров, но и для
заряженных тел произвольной формы,
расположенных на большом
расстоянии
друг от друга: приращение электрической
энергии системы равно приращению энергии
взаимодействия заряженных тел системы:
электрическая энергия взаимодействия
существенно меньше суммы собственных
энергий шаров, однако при изменении
расстояния между шарами собственные
энергии остаются практически постоянными
и изменение полной электрической энергии
примерно равно изменению энергии
взаимодействия. Этот вывод справедлив
не только для проводящих шаров, но и для
заряженных тел произвольной формы,
расположенных на большом
расстоянии
друг от друга: приращение электрической
энергии системы равно приращению энергии
взаимодействия заряженных тел системы:
 .
Энергия взаимодействия
.
Энергия взаимодействия
 удаленных друг от друга тел не зависит
от их формы и определяется формулой
(2).
удаленных друг от друга тел не зависит
от их формы и определяется формулой
(2).
При выводе формул (1), (2) каждый из точечных зарядов рассматривался как нечто целое и неизменное. Учитывалась только работа, совершаемая при сближении таких неизменных зарядов, но не на их образование. Напротив, при выводе формул (3), (4) учитывалась также работа, совершаемая при нанесении зарядов q i на каждое из тел системы путем переноса электричества бесконечно малыми порциями из бесконечно удаленных точек. Поэтому формулы (3), (4) определяют полную электрическую энергию системы зарядов, а формулы (1), (2) только электрическую энергию взаимодействия точечных зарядов.
Объемная плотность энергии электрического поля
Электрическую энергию плоского конденсатора можно выразить через напряженность поля между его обкладками:
 ,
,
где
 -
объем пространства, занятого полем,
S
– площадь обкладок, d
– расстояние
между ними. Оказывается, через напряженность
можно выразить электрическую энергию
и произвольной системы заряженных
проводников и диэлектриков:
-
объем пространства, занятого полем,
S
– площадь обкладок, d
– расстояние
между ними. Оказывается, через напряженность
можно выразить электрическую энергию
и произвольной системы заряженных
проводников и диэлектриков:
 ,
(5)
,
(5)
 ,
,
а интегрирование
проводится по всему пространству,
занятому полем (предполагается, что
диэлектрик изотропный и
 ).
Величина w
представляет собой электрическую
энергию, приходящуюся на единицу объема.
Вид формулы (5) дает основания предположить,
что электрическая энергия заключена
не во взаимодействующих зарядах, а в их
электрическом поле, заполняющем
пространство. В рамках электростатики
это предположение проверить экспериментально
или обосновать теоретически невозможно,
однако рассмотрение переменных
электрических и магнитных полей позволяет
удостоверится в правильности такой
полевой интерпретации формулы (5).
).
Величина w
представляет собой электрическую
энергию, приходящуюся на единицу объема.
Вид формулы (5) дает основания предположить,
что электрическая энергия заключена
не во взаимодействующих зарядах, а в их
электрическом поле, заполняющем
пространство. В рамках электростатики
это предположение проверить экспериментально
или обосновать теоретически невозможно,
однако рассмотрение переменных
электрических и магнитных полей позволяет
удостоверится в правильности такой
полевой интерпретации формулы (5).
Лекция 2.6.
Энергия взаимодействия зарядов
Рассмотрим систему из двух точечных зарядов. Энергию взаимодействия можно трактовать как энергию первого заряда в поле второго (cм.(2.1.3))
Поскольку оба представления равноправны, энергию взаимодействия этих зарядов можно записать следующим образом
где - i -тый точечный заряд системы, - потенциал поля, созданного всеми остальными зарядами системы, кроме i -того, в точке расположения заряда .
Если заряды распределены непрерывно, то, представляя систему зарядов как совокупность элементарных зарядов и переходя к интегрированию, получим выражение
где - энергия взаимодействия друг с другом элементарных зарядов первого шарика, - энергия взаимодействия друг с другом элементарных зарядов второго шарика, - энергия взаимодействия элементарных зарядов первого шарика с элементарными зарядами второго шарика. Энергии и называют собственными энергиями зарядов и . Энергию называют энергией взаимодействия зарядов и .
Энергия уединенного проводника и конденсатора
Пусть проводник имеет заряд и потенциал . Энергия проводника . Поскольку проводник является эквипотенциальной областью, то потенциал выносится из-под знака интеграла. Окончательно
Энергия конденсатора.
Пусть и - заряд и потенциал положительно заряженной обкладки, а и - соответственно отрицательной. Тогда энергия конденсатора с учетом и запишется
Энергия электрического поля.
Физический смысл энергии конденсатора это не что иное, как энергия электрического поля сосредоточенного внутри него . Получим выражение для энергии плоского конденсатора через напряженность. Будем пренебрегать краевыми эффектами. Воспользуемся формулой , и выражением для емкости плоского конденсатора .
Подынтегральное выражение здесь имеет смысл энергии, заключенной в объеме. Это подводит к важной идее о локализации энергии в самом поле.
Это предположение находит подтверждение в области переменных полей. Именно переменные поля могут существовать независимо от возбудивших их электрических зарядов и распространяться в пространстве в виде электромагнитных волн, которые переносят энергию.
Таким образом, носителем энергии является само поле .
Анализируя последнее выражение, можем ввести объемную плотность энергии, т.е. энергии, заключенной в единице объема
| . | (2.6.9) |
Мы получили (2.6.8) и (2.6.9) в частном случае однородного, изотропного диэлектрика в однородном электрическом поле. В этом случае векторы и сонаправлены и можно записать